题目分析
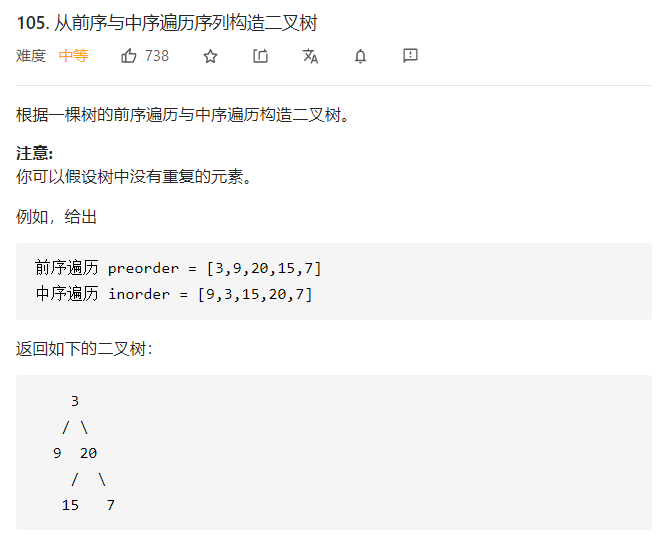
二叉树的遍历是笔试中常考的题型,经常出现在选择或者填空题之中,相关的知识可以参考二叉树的遍历相关博客,这个题目是根据前序和中序遍历如何反推出一颗树,我认为很有价值,因此推荐给小伙伴们学习。
递归
我们已知了前序遍历,因此前序遍历的第一个节点就是当前二叉树的根节点,我们再从中序遍历中找到该节点,那么中序遍历左边的节点都是左子树,中序遍历右边的节点都是右子树。然后根据左子树的节点个数,确定左子树和右子树的前序遍历,递归建树即可。
算法的**时间复杂度为$O(n)$,空间复杂度为$O(n)$**。
1 | class Solution(object): |
刷题总结
题目的难点在于如何根据根节点确定左右子树的前序和中序遍历,难度不大,需要仔细想一想其中的逻辑关系。